Abstract

Given the problem of a restricted access corpus where full texts cannot be stored locally, we propose to make use of the fact that the skip gram algorithm operates on bigrams to train a word embedding model on as little as a word-context-frequency matrix in a highly memory-efficient way.

Preamble

An important aspect of the WE1S ethos is its sense of pragmatism. We deliberately engage with the gritty technical, legal, and social conditions of research that are inseparable from the questions we hope to answer. For example, a substantial portion of the WE1S corpus that we plan to data mine is constituted by newspaper articles. While many of these media sources are made available for scholarly research through proprietary databases, a combination of technical, copyright, and contractual restrictions limit how we can store or use full texts. Rather than treat these technical and legal constraints as obstacles to research, however, we prefer to see them as opportunities to engage with the very conditions of our knowledge. How does WE1S fit into, draw from, and intervene in the situations in which it is embedded? This blog post proposes a solution to one such intersection of technical and legal constraints as it arose during our implementation of algorithms for word embedding analysis. The problem of full-text access is a familiar one in the Digital Humanities, and we believe that our solution will be of interest to the scholarly community.

Problem

The research methods of WE1S are built primarily around data mining. That is, we plan to use computational techniques, such as topic modeling and word embedding, in order to analyze our corpus of public discourse on the humanities. But, of course, data mining first requires that we collect the data and process it into an appropriate format. The format of our data simultaneously raises legal and technical problems.

The most popular word embedding algorithm today, by far, is word2vec (Mikolov 2013). Briefly, word2vec is an efficient technique for producing word embeddings using on a shallow neural net architecture. The embeddings it produces achieve state-of-the-art performance on tests of semantic representation, and the algorithm itself runs quickly and uses only a small amount of memory. Although word2vec had appeared to be a natural choice as one of our research methods, its pre-processing became an obstacle. Popular implementations of word2vec, such as in gensim for Python, require full-text access. Entire sentences are passed into the algorithm at once, in order to efficiently collect keywords and their contexts. Unfortunately, copyright law and the terms and conditions of many of our database sources prevent us from storing full texts in our database. In general, WE1S thus stores “non-consumptive use,” processed versions of its texts to hard disk in order to reproduce and validate findings. Such materials are not in the form that word2vec algorithms most widely accept.

In order to sidestep this problem, we attempted to implement an alternate word embedding algorithm with different pre-processing requirements. There is an older generation of algorithm that uses simple bigram frequencies as the basis for its embeddings, and that has been recently demonstrated to achieve near state-of-the-art performance on many semantic tests (Levy et al. 2015). These techniques are based on calculations of mutual information conveyed by each keyword-context word pair. (In particular, we implemented the positive pointwise mutual information embeddings and their singular value decomposition, as described in Levy et al.). However, when we piloted our mutual information-based embeddings we encountered memory problems. The raw matrix — a square with rows and columns equal to the number of words in our vocabulary — was too big for our consumer-grade hardware. Even when we handled it as a sparse matrix (only an ordered set of non-zero values), the processing was terribly inefficient.

Copyright law, contractual restraints, and cost of hardware had conspired to constrain our use of software and, indeed, our scholarly research methods.

Solution

Other than commonly assumed, however, not all word embedding algorithms require a “scan” of the full text. Most prominently, the popular skip gram algorithm (Mikolov 2013) (with or without negative sampling), while keeping the idea of training a word-to-context mapping, internally operates on bigrams. In the original formulation (Mikolov 2013) define Skip-gram as a maximization of the average log probability

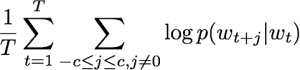
where c is the size of the training context, and w₁, w₂, …, w_T is a sequence of words, for instance a sentence. The training set for this sequence then consists of all possible bigrams in the context window c. For instance, for the sentence “The quick brown fox jumps over the lazy dog”, and a context window size of 3, the set of training samples would consist of the bigrams (the|quick), (the|brown), (the|fox), (quick|the), (quick|brown), and so on. Importantly, the addition of any of the improvements proposed in (Mikolov 2013, Levy 2015), like negative sampling, subsampling, or dynamic windowing, does not change the algorithm’s use of bigrams.

To train a word embedding using skip-gram, all that is necessary is thus the list of all possible bigrams for all possible context windows. This list can be stored as a word-context-frequency matrix of size v² where v is the size of the vocabulary. A text stored as such a matrix cannot be reconstructed, as word order is not preserved. This means: by utilizing skip-gram in combination with a word-context-frequency matrix, restricted access corpora can be used to train word embedding models without the need to keep local copies of the full texts, either by storing one word-context-matrix for each text, or by adding the frequency counts for multiple texts together.

A great side effect is that memory use becomes independent of text size, as only the size of the vocabulary (which has a natural maximum but is usually restricted to ~10,000 words) affects the size of the word-context-frequency matrix.

Implementation

Our implementation uses the Keras machine learning framework to train the embedding. First, the full text is transformed into a word-context-frequency matrix. The matrix is then transformed into a sparse matrix internally to save even more memory. During each training epoch, a generator randomly samples the matrix until it is “empty”. Negative samples are added on the fly according to a user-defined hyperparameter. After the end of the epoch, the original matrix is restored, and the process starts again. After training, the embedding is stored in a Gensim and TensorFlow embedding projector compatible format for further exploration. The implementation also makes use of subsampling (Mikolov 2013) and dynamic windowing (Levy 2015).

A Jupyter notebook for the implementation can be found here. Please note that this is a prototype implementation, designed to work on specific test corpora. Good hyperparameters will be significantly different for larger/different corpora.

Contact Fabian Offert (@haltingproblem) for more information.

References

Levy, Omer, Yoav Goldberg, and Ido Dagan. “Improving Distributional Similarity with Lessons Learned from Word Embeddings.” Transactions of the Association for Computational Linguistics 3 (2015): 211–25.